
克雷西 发自 凹非寺证券配资炒股
量子位 | 公众号 QbitAI
AI已经能够自主思考并证明新的数学规律了?
OpenAI研究人员表示,自己喂给GPT-5 Pro一篇论文,结果模型读完之后得到了新的结论。
在凸优化问题当中,GPT-5 Pro针对一个边界问题,给出了比原文更加精确的阈值和相应证明。
消息立即引发全网热议,不到半天推文就有230多万次阅读。
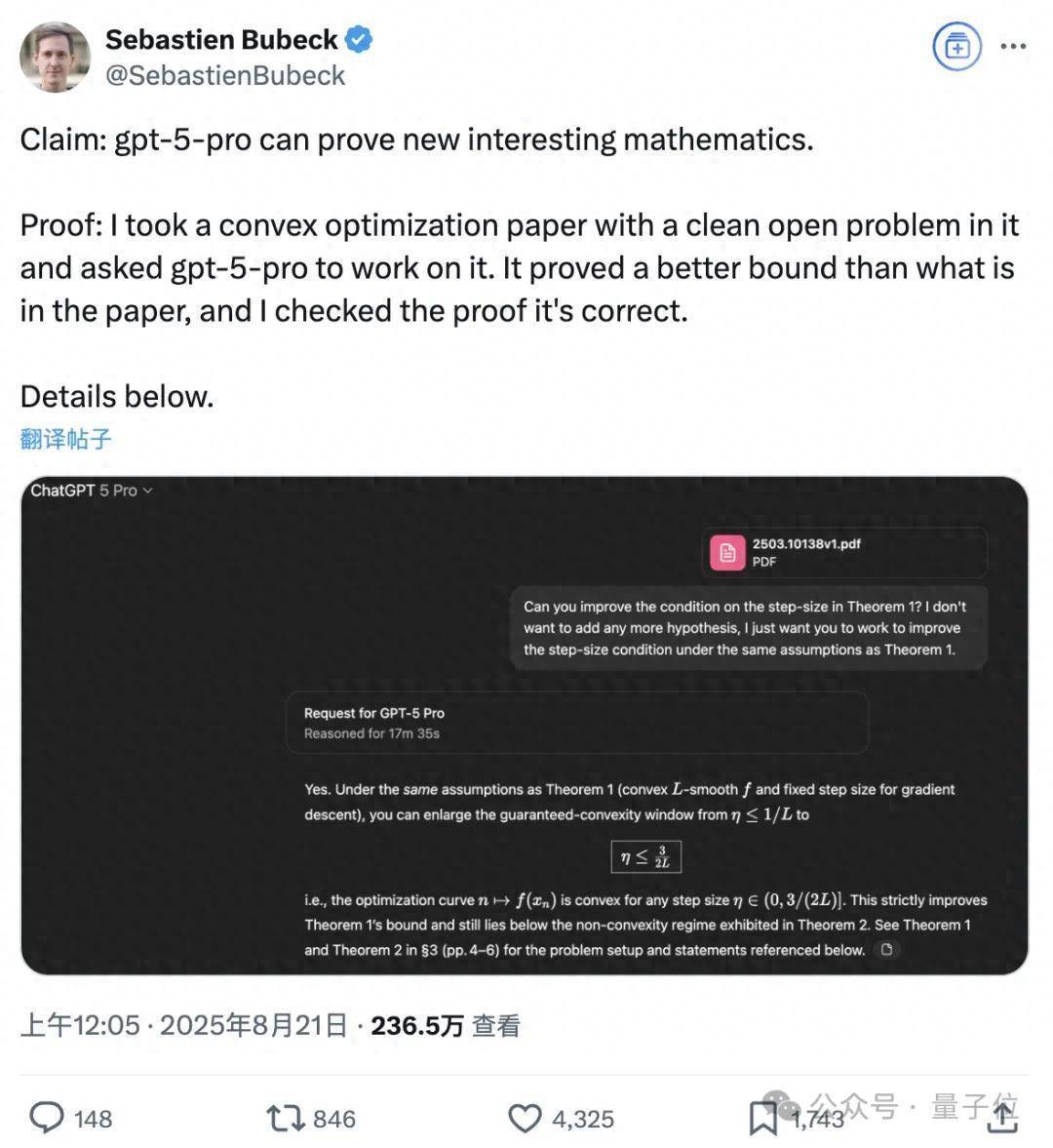
不过这位研究人员并没有将GPT-5 Pro的研究成果发表成论文,理由是被人类抢先了——
这篇论文后来又更新了一个版本,给出了新的边界,这个新的边界又把GPT-5 Pro反超了。
但是,GPT-5 Pro的证明思路与此并不相同,说明它已经具备了独立探索的能力,所以人类的反攻也不影响这是GPT-5 Pro的一个新突破。
OpenAI总裁Brockman甚至将这一成果称之为“生命迹象”。
凸优化曲线是凸的吗?
喂给GPT-5 Pro的这篇另论文,研究的是凸优化(convex optimization)问题,凸优化是数学最优化的一个子领域,研究定义于凸集中的凸函数最小化的问题。
具体来说,这篇论文题目为《凸优化曲线是凸的吗?》,研究了这样的一个问题:
当使用梯度下降算法优化光滑凸函数时,其产生的优化曲线(optimization curve)是否是凸的?
这里的“优化曲线”指的是函数值f(x_n)随迭代次数n变化的曲线。如果这条曲线是凸的,意味着优化速率(即相邻两次迭代的函数值下降量)是单调递减的。
关于这个问题证券配资炒股,论文的结论是优化曲线凸不凸,关键取决于步长(step size)的选择,具体包括如下几个关键点:
凸性保证区间:当步长η ∈ (0, 1/L]时(L为平滑度),优化曲线保证是凸的;非凸可能区间:当步长η ∈ (1.75/L, 2/L)时,即使梯度下降仍单调收敛,优化曲线可能不是凸的;梯度范数性质:对于整个收敛区间η ∈ (0, 2/L],梯度范数序列网配查提示:文章来自网络,不代表本站观点。